不确定性原理，又叫做测不准原理;不确定原理，外文名叫做Uncertainty principle，提出时间是在1927年，提出者是维尔纳·海森堡。

　　历史

　　1925年6月，海森堡在论文《运动与机械关系的量子理论重新诠释》(Quantum-Theoretical Re-interpretation of Kinematic and Mechanical Relations)里表述出矩阵力学 。从此旧量子论渐趋式微，现代量子力学的时代正式开启。矩阵力学大胆地假设，经典的运动概念不适用于量子层级，束缚在原子内部的电子并不具有明确定义的轨道，而是运动于模糊不清，无法观察到的轨道，其对于时间的傅里叶变换只涉及到因量子跃迁而产生的可以被观察到的电磁辐射的离散频率。

　　海森堡在论文里提出，只有在实验里能够观察到的物理量才具有物理意义，才可以用理论描述其物理行为，其它都是无稽之谈。因此，他刻意避开任何涉及粒子运动轨道的详细计算，例如，粒子随着时间而改变的确切运动位置，因为，这运动轨道是无法直接观察到的，替代地，他专注于研究电子跃迁时，所发射出的电磁辐射的离散频率和强度。他计算出代表位置与动量的无限矩阵。这些矩阵能够正确地预测电子跃迁所发射出光波的强度。

　　同年6月，在阅读了海森堡的论文之后，马克斯·玻恩发现，海森堡的数学运算原来就是他在学生时代学到的 矩阵微积分 ( 英语 ： matrix calculus ) ，另外，在分别表示位置与动量的两个无限矩阵之间存在着一种很特别的关系──正则对易关系，以方程表示为 ：

　　但是，他们并不了解这重要结果的意义，他们无法给予合理的诠释。

　　海森堡与玻尔共同讨论问题

　　1926年，海森堡任聘为哥本哈根大学尼尔斯·玻尔研究所的讲师，协助尼尔斯·玻尔做研究。隔年，他发表了论文《论量子理论运动学与力学的物理内涵》(On the physical content of quantum theoretical kinematics and mechanics)。在这篇论文里，他严格要求遵守实证主义：只有在可以设定的实验环境下对于粒子的某种数量做测量，则这数量才具有物理意义，否则这数量不具有任何物理意义。 他接着解释，任何实验测量都会遭遇误差，因此，这数量的物理意义也只能被确定至某种程度。例如，假设使用显微镜来测量粒子的位置，对于粒子的位置的测量会不可避免地搅扰了粒子的动量，造成动量的不确定性。海森堡紧跟着给出他的不确定性原理：越精确地知道位置，则越不精确地知道动量，反之亦然。不确定性原理能够直接地诠释位置与动量的正则对易关系：假若测量位置不会搅扰动量，测量动量不会搅扰位置，则测量位置与动量不需要顾虑到先后关系，位置与动量的正则对易关系会变为 [ x , p ] = x p − − --> p x = 0 {\displaystyle [x,\,p]=xp-px=0} 。

　　在这篇论文里， 海森堡写出公式

　　这公式给出了任何位置测量所造成的最小无法避免的动量不确定值，但是他没有给予 Δ Δ --> x {\displaystyle \Delta x} 和 Δ Δ --> p {\displaystyle \Delta p} 确切的定义。在海森堡的芝加哥讲义里，他又进一步改善了这关系式：

　　1927年， 厄尔·肯纳德 ( 英语 ： Earl Kennard ) 首先证明了现代不等式 ：

　　其中， Δ Δ --> x {\displaystyle \Delta x} 是位置标准差， Δ Δ --> p {\displaystyle \Delta p} 是动量标准差， ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数。

　　海森堡只给出关于高斯波包案例的不等式。

　　1929年， 霍华德·罗伯森 ( 英语 ： Howard Robertson ) 推导出基于对易关系的不确定关系式。

　　三种表述

　　不确定性原理主要有三种表述：

　　顺序测量不确定性原理：不可能在测量位置时完全不搅扰动量，反之亦然。

　　联合测量不确定性原理：不可能对于位置与动量做 联合测量 ( 英语 ： joint measurement ) ，即同步地测量位置与动量，只能做近似联合测量。

　　制备不确定性原理：不可能制备出量子态具有明确位置与明确动量的量子系统。

　　很多学者主张，追根究柢，这三种表述等价，可以从其中任意一种表述推导出另一种表述，然而，在这方面的论述，并不很明确。

　　顺序测量不确定性原理

　　顺序测量不确定性原理表明，对于粒子位置的测量不可避免地搅扰了粒子的动量(这结论可以从海森堡显微镜实验获得)，以方程表示，

　　其中， Δ Δ --> x m e a s u r e {\displaystyle \Delta x_{measure}} 是测量位置所出现的误差， Δ Δ --> p p e r t u r b {\displaystyle \Delta p_{perturb}} 是动量被测量位置的动作所搅扰才出现的误差。

　　反之亦然，对于粒子动量的测量不可避免地搅扰了粒子的位置(这结论可以从 多普勒速率表实验 ( 英语 ： Doppler speed meter experiment ) 获得)，以方程表示，

　　其中， Δ Δ --> p m e a s u r e {\displaystyle \Delta p_{measure}} 是测量动量所出现的误差， Δ Δ --> x p e r t u r b {\displaystyle \Delta x_{perturb}} 是位置被测量动量的动作所搅扰才出现的误差。

　　顺序测量不确定性原理时常会被曲解，有些人认为，由于测量仪器有技术瑕疵，才会得到与不确定性原理相符合的结果，假若能够使用更精良的仪器，应该可以获得违背不确定性原理的结果。但这想法并不正确，当初海森堡表述不确定性原理时，他设计的海森堡显微镜实验是一种思想实验，其所使用的是假想最精良的仪器，在假想最理想的环境里工作，因此，对于在微观世界里的测量动作，由不确定性原理所规定的基于普朗克常数的限制是无法突破的。

　　任何科学理论都必须通过严格实验验证，否则只能视为伪科学。海森堡并没有对于不确定性原理给出任何实验验证。由于严格实验验证需要非常精良的仪器，直到近期，才有实验达成测试不确定性原理的目标。

　　海森堡显微镜实验

　　海森堡假想测量电子(蓝点)位置的伽马射线显微镜。波长为 λ λ --> {\displaystyle \lambda } 的侦测伽马射线(以绿色表示)，被电子散射后，进入孔径角为 2 θ θ --> {\displaystyle 2 heta } 的显微镜的透镜，其直径为 D {\displaystyle D} 。散射后的伽马射线以红色表示。

　　海森堡主张，只有在可以设定的实验环境下对于粒子的位置做测量，则位置才具有物理意义，否则位置不具有任何物理意义。为了展示怎样测量位置以及会产生什么样的后续状况，海森堡设计出伽马射线显微镜思想实验 。在这实验里，一束光线被照射于一个电子，然后用显微镜的透镜来搜集被电子散射的光线，从而获得电子的位置数据。光线的波长越短，可以越准确地测量电子位置，但是，光线的动量也会变大，而且会因为被散射而传输动量给电子，其数量无法被确定。波长越长的光线，动量越小，电子的动量不会因为散射而大大地改变。可是，电子的位置也只能大约地被测知。根据经典光学理论，透镜的 分辨本领 ( 英语 ： resolving power ) 为

　　其中， Δ Δ --> x {\displaystyle \Delta x} 是电子位置的不确定性， λ λ --> {\displaystyle \lambda } 是光线的波长， θ θ --> {\displaystyle heta } 是孔径角。

　　假设光线被散射进入显微镜的透镜，则它的轨迹与透镜的光轴两者之间的夹角角弧必小于 θ θ --> {\displaystyle heta } ，它的动量大约与原本动量 p {\displaystyle p} 相同 ，垂直于光轴的动量分量必小于 p sin ⁡ ⁡ --> ( θ θ --> ) {\displaystyle p\sin( heta )} ，由于不知道轨迹与光轴的夹角角弧，因此无法计算出 Δ Δ --> p x {\displaystyle \Delta p_{x}} 的确切数值。按照动量守恒定律，光线所失去的动量是电子所增添的动量，所以电子动量因被光线散射而产生的不确定性 Δ Δ --> p x {\displaystyle \Delta p_{x}} 约为

　　综合上述两个方程，可得到与孔径角无关的公式

　　这公式是从两个经典理论求得，完全没有用到任何量子理论。在经典力学里，若要减小乘积 Δ Δ --> x Δ Δ --> p x {\displaystyle \Delta x\Delta p_{x}} ，有两种方法，一是使用波长越短的光线越好，这意味着使用伽马射线，二是减低辐照度，因为电磁辐射的动量与辐照度成正比。若能促使波长越短，辐照度越低，则乘积 Δ Δ --> x Δ Δ --> p x {\displaystyle \Delta x\Delta p_{x}} 就会变得越小，没有任何基础限制对于不确定性乘积给出约束。然而，在量子力学里，当辐照度降低到某种程度时，必须要将光的颗粒性纳入考量，必须思考一个光子与一个电子相遇时所发生的康普顿散射，根据德布罗意假说，

　　将这公式带入乘积 Δ Δ --> x Δ Δ --> p x {\displaystyle \Delta x\Delta p_{x}} 的公式，可以得到海森堡的不确定性关系式

　　在这实验里，被测量的物理量是位置， Δ Δ --> x {\displaystyle \Delta x} 是测量误差 Δ Δ --> x m e a s u r e {\displaystyle \Delta x_{measure}} ，而被搅扰的物理量是动量， Δ Δ --> p x {\displaystyle \Delta p_{x}} 是搅扰误差 Δ Δ --> p p e r t u r b {\displaystyle \Delta p_{perturb}} ，因此，

　　在经典力学里，在测量物体时，搅扰可以被消减得越小越好，但在量子力学里，对于这搅扰存在着一个基础限制，并且，这搅扰无法被控制、无法被预测、无法被修正。海森堡显微镜实验创新地给出这限制 。

　　至此，海森堡的论述仍旧不完整，他尚未解释怎样获知粒子的动量。假若能测量到粒子的动量，才能给予粒子的动量实际意义，否则，粒子的动量不具意义，“粒子的动量被搅扰”这句话也不具意义。更多内容，请查阅条目海森堡显微镜实验。

　　单狭缝衍射

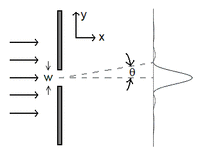
　　单狭缝实验示意图。

　　粒子的波粒二象性的概念可以用来解释位置不确定性和动量不确定性的关系。自由粒子的波函数为平面波。假设，这平面波入射于刻有一条狭缝的不透明挡板，平面波会从狭缝衍射出去，在档墙后面的侦测屏，显示出干涉图样。根据单狭缝衍射公式，从中央极大值位置(最大波强度之点)到第一个零点(零波强度之点)的夹角 θ θ --> {\displaystyle heta } 为

　　其中， λ λ --> {\displaystyle \lambda } 是平面波的波长， w {\displaystyle w} 是狭缝宽度。

　　给定平面波的波长，狭缝越窄，衍射现象越宽阔， θ θ --> {\displaystyle heta } 越大;狭缝越宽，衍射现象越窄缩， θ θ --> {\displaystyle heta } 越小。

　　当粒子穿过狭缝之前，在粒子前进的方向(x方向)的动量为 p {\displaystyle p} ，在y方向的动量 p y {\displaystyle p_{y}} 是零。穿过狭缝时，粒子的动量遭遇搅扰。 p y {\displaystyle p_{y}} 的不确定性 Δ Δ --> p y {\displaystyle \Delta p_{y}} 大约是

　　当粒子穿过狭缝时，粒子的位置不确定性 Δ Δ --> y {\displaystyle \Delta y} 是狭缝宽度： Δ Δ --> y ≈ ≈ --> w {\displaystyle \Delta y\approx w} 。

　　所以，位置不确定性与动量不确定性的乘积大约为

　　从德布罗意假说，

　　所以，位置不确定性与动量不确定性遵守近似式

　　在这实验里，被测量的物理量是位置， Δ Δ --> y {\displaystyle \Delta y} 是测量误差 Δ Δ --> y m e a s u r e {\displaystyle \Delta y_{measure}} ，而被搅扰的物理量是动量， Δ Δ --> p y {\displaystyle \Delta p_{y}} 是搅扰误差 Δ Δ --> p p e r t u r b {\displaystyle \Delta p_{perturb}} ，因此，

　　联合测量不确定性原理

　　联合不确定性原理表明，不可能对于位置与动量做 联合测量 ( 英语 ： joint measurement ) ，即同步地测量位置与动量，只能做出近似联合测量，其误差遵守不等式

　　其中， Δ Δ --> x {\displaystyle \Delta {x}} 与 Δ Δ --> p {\displaystyle \Delta {p}} 分别为位置与动量的测量误差。

　　假设一个量子系统的两个可观察量A、B是另外一个可观察量C的函数，即A=f(C)与B=g(C)，则称可观察量A、B可以被“联合测量”(又称为同步测量)。 假若两种可观察量的对易算符不等于0，即它们不相互对易，则称它们为“不相容可观察量”。联合测量两个不相容可观察量是不可行的。

　　在经典力学里，可以同步测量宏观物体的位置与动量，但是，量子力学的标准形式论不准许联合测量粒子的位置与动量，这是因为标准形式论的可观察量不具备这种功能。近期，物理学者将标准形式论加以延伸，提出 正值算符测度 ( 英语 ： positive-operator valued measure ) 的理论，正值算符测度可以用来表述联合测量。但是，在这里每一种测量都必须是 模糊测量 ( 英语 ： unsharp measurement ) ，换句话说，联合准确测量(同步准确测量)粒子的位置与动量是不可行的，因为粒子的位置与动量是不相容可观察量。

　　制备不确定性原理

　　制备不确定性原理指出，不可能制备出量子态具有任意明确位置与任意明确动量的量子系统，换句话说，所有制备出的量子系统，其量子态的位置与动量必须遵守不等式

　　其中， σ σ --> x {\displaystyle \sigma _{x}} 与 σ σ --> p {\displaystyle \sigma _{p}} 分别为位置与动量的标准差， ℏ ℏ --> {\displaystyle \hbar } 是约化普朗克常数。

　　从制备量子系统的角度来看，设想一个量子系统被复制成很多份，每一份系统都是用同样方法制备而成，那么，它们都具有同样的量子态，总称它们为一个系综，因此，量子态代表一个系综的同样方法制备出来的量子系统。现在对每一份系统测量任意可观察量A，一般而言，这些测量会得到不同的结果，它们形成了一种概率分布。从量子态计算出来的可观察量A的理论概率分布，在复制数量趋于无穷大的极限，会与测量实验所获得可观察量A概率分布完全一致。

　　量子系统的物理行为可以用波函数来描述，波函数的绝对值平方是量子系统的概率分布。概率分布的宽度或扩展可以用标准差或某种测度来量度。波函数也可以用来计算出位置或动量的概率分布，从而获得以位置与动量的标准差来表达的不确定性关系式。这关系式表达出符合量子力学对于制备量子系统所设定的限制，是制备不确定性原理的表达式。 由同样方法制备而成的多个量子系统，它们会具有的某些类似的性质，但也会具有某些不同的性质，它们所具有的性质不可能每一种都相同。"

　　平面波波包德布罗意波的1维传播，复值波幅的实部以蓝色表示、虚部以绿色表示。在某位置找到粒子的概率(以颜色的不透明度表示)呈波形状延展。

　　在波动力学里，波函数描述粒子的量子行为。在任意位置，波函数的绝对值平方是粒子处于那位置的概率;概率越高，则粒子越常处于那位置。动量则与波函数的波数有关。

　　根据德布罗意假说，物质具有波动性质，会展示出像物质波一般的物理性质，因此，粒子的位置可以用波函数 Ψ Ψ --> ( x , t ) {\displaystyle \Psi (x,t)} 来描述。假设这波函数的空间部分 ψ ψ --> ( x ) {\displaystyle \psi (x)} 是单色平面波，以方程表示

　　其中， k 0 {\displaystyle k_{0}} 是波数， p 0 {\displaystyle p_{0}} 是动量。

　　玻恩定则表明，波函数可以用来计算概率，在位置 a {\displaystyle a} 与 b {\displaystyle b} 之间找到粒子的概率 P {\displaystyle P} 为

　　对于单色平面波案例， | ψ ψ --> ( x ) | 2 {\displaystyle |\psi (x)|^{2}} 是均匀分布，这粒子的位置极端不确定，因为，它在 a {\displaystyle a} 与 b {\displaystyle b} 之间任意位置的概率都一样。

　　如右图所示，思考一个由很多正弦波叠加形成的波函数：

　　其中， A n {\displaystyle A_{n}} 是 p n {\displaystyle p_{n}} 模的振幅。

　　取连续性极限，波函数是所有可能模的积分：

　　其中， ϕ ϕ --> ( p ) {\displaystyle \phi (p)} 是模的振幅，称为动量空间的波函数。

　　以数学术语表达， ψ ψ --> ( x ) {\displaystyle \psi (x)} 的傅里叶变换是 ϕ ϕ --> ( p ) {\displaystyle \phi (p)} ，位置 x {\displaystyle x} 与动量 p {\displaystyle p} 是共轭物理量。将这些平面波叠加在一起的副作用是动量的不确定性变大， ψ ψ --> ( x ) {\displaystyle \psi (x)} 是很多不同动量的平面波组成的混合波。标准差 σ σ --> {\displaystyle \sigma } 定量地描述位置与动量的不确定性。粒子位置的概率密度函数 | ψ ψ --> ( x ) | 2 {\displaystyle |\psi (x)|^{2}} 可以用来计算标准差。使用更多平面波，可以减低位置的不确定性，即减低 σ σ --> x {\displaystyle \sigma _{x}} ，但也因此增加动量的不确定性，即增加 σ σ --> p {\displaystyle \sigma _{p}} 。这就是不确定性原理。