柯西-黎曼方程,外文名Cauchy-Riemann Equations,简称C-R方程,是提供了可微函数在开集中为全纯函数的充要条件的两个偏微分方程,最早出现在达朗贝尔的著作中。
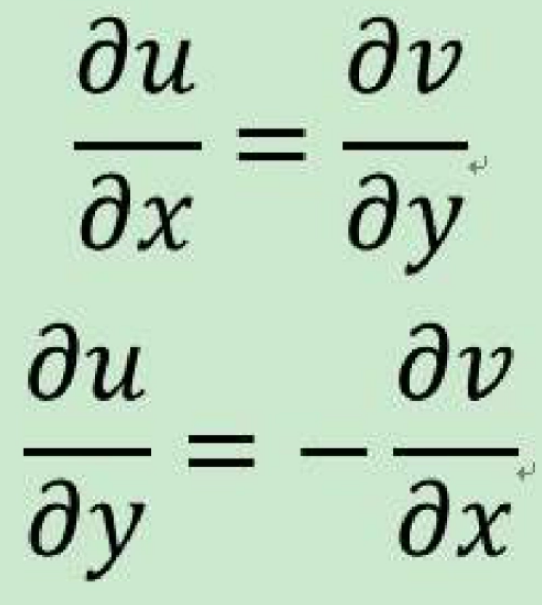
注释和其他表述
共形映射
柯西-黎曼方程常常表述为其他形式。首先,它们可以写成复数形式:
在此形式中,方程对应于雅可比矩阵结构上有如下形式
其中a=∂ ∂ -->u/∂ ∂ -->x=∂ ∂ -->v/∂ ∂ -->y{⁄displaystyle ⁄scriptstyle a=⁄partial u/⁄partial x=⁄partial v/⁄partial y},b=∂ ∂ -->v/∂ ∂ -->x=− − -->∂ ∂ -->u/∂ ∂ -->y{⁄displaystyle ⁄scriptstyle b=⁄partial v/⁄partial x=-⁄partial u/⁄partial y}。该形式的矩阵是复数的矩阵表示。几何上,这样的一个矩阵总是一个旋转和一个缩放的复合,从而是保角(保持角度不变)的。因此,满足柯西-黎曼方程的有非零导数的函数保持平面曲线的角度不变。也即,柯西-黎曼方程是函数成为共形映射的条件。
复共轭的独立性
方程组有时也被写作一个方程
其中微分算子∂ ∂ -->∂ ∂ -->z¯ ¯ -->{⁄displaystyle {⁄frac {⁄partial }{⁄partial {⁄bar {z}}}}}定义为
在此形式中,柯西-黎曼方程可以解释为f独立于变量z¯ ¯ -->{⁄displaystyle {⁄bar {z}}}。
复可微性
柯西-黎曼方程是函数的复可微性(或称全纯性)的充要条件(Ahlfors 1953,§1.2)。精确的讲,设
为复数z∈C的函数,则f在点z0的复导数定义为
如果该极限存在。
若该极限存在,则可以取h→0沿着实轴或者虚轴的极限;它在两种情况下应该给出同样的结果。从实轴逼近,得到
而从虚轴逼近有
f沿着两个轴的导数相同也即
这就是在点z0的柯西-黎曼方程(2)。
反过来,如果f:C → C作为映射到R上的函数可微,则f复可微当且仅当柯西-黎曼方程成立。
物理解释
柯西-黎曼方程的一个解释(Pólya & Szegö 1978)和复变理论无关。设u和v在R的开子集上满足柯西-黎曼方程,考虑向量场
将其视为(实)两个分量的向量。则第二个柯西-黎曼方程(1b)断言f¯ ¯ -->{⁄displaystyle {⁄bar {f}}}无旋:
第一个柯西-黎曼方程(1a)断言该向量场无源(或者是零散度):
分别根据格林定理和散度定理,这样的场是保守的,而且没有源,在整个开域上净流量为零。(这两点在柯西积分定理中作为实部和虚部结合起来。)在流体力学中,这样的一个场是一个势流(Chanson 2000)。在静磁学中,这样的向量场是在不含电流的平面区域中的静磁场的模型。在静电学中,它们提供了不包含电荷的平面区域的电场模型。
其它解释
柯西-黎曼方程的其他表述有时出现在其他坐标系中。若(1a)和(1b)对于连续函数u和v成立,则如下方程也成立
对于任何坐标(n(x,y), s(x,y)),如果它们满足(∇ ∇ -->n,∇ ∇ -->s){⁄displaystyle ⁄scriptstyle (⁄nabla n,⁄nabla s)}正交并且正定向。因此,特别的有,在极坐标z=re下,方程组有如下形式
结合成一个f的方程,就有
非齐次方程
非齐次柯西-黎曼方程由两个未知两个实变量的函数u(x,y)和v(x,y)的方程组成
对于给定的定义在R的开子集上的函数α(x,y)和β(x,y)。这些方程经常合并为一个方程。
其中f=u+iv,φ=(α+iβ)/2。
若φ是Ck的,则在有界区域D中方程显式可解,只要φ在D的闭包上连续。实际上,按照柯西积分公式,
对于所有ζ∈D成立。
推广
Goursat定理及其推广
设f = u+iv为复函数,作为函数f : R → R可微。则柯西积分定理(柯西-古尔萨定理)断言f在开复域Ω上解析当且仅当它在该域上满足柯西-黎曼方程(Rudin 1966,Theorem 11.2)。特别是,f不需假定为连续可微(Dieudonné 1969,§9.10, Ex. 1)。
柯西-古尔萨定理的假设可以大幅减弱;f不需可微,只要f=u+iv在Ω上连续且f关于x和y的偏导数在Ω中存在即可,这个结果称为Looman–Menchoff定理。
f在整个域Ω上满足柯西-黎曼方程是要点。可以构造在一点满足柯西-黎曼方程的连续函数,但它不在该点解析(譬如,f(z) = z/|z|)。只满足柯西-黎曼方程也是不够的,(需额外满足连续性),下面的例子表明了这一点:(Looman 1923,p.107)
它处处满足柯西-黎曼方程,但在z=0不连续。
但是,如果一个函数在开集上以弱形式满足柯西-黎曼方程,则函数解析。更精确的讲(Gray & Morris 1978,Theorem 9):
若f(z)在开域Ω⊂C上局部可积,并以弱形式满足柯西-黎曼方程,则f和Ω上的一个解析函数几乎处处相等。
多变量的情况
在多复变量的理论中有对柯西-黎曼方程的恰当推广。他们组成一个偏微分方程的严重过约束系统。通常的表述中,d-bar算子
将全纯函数消零。这是
的直接推广 其中
参看
复分析主题列表