祖暅(456年-536年),又名祖暅之,祖冲之之子,中国南北朝时期天文学家、数学家。
个人简介
祖冲之父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同则积不容异”,即等高的两立体,若其任意高处的水平截面积相等,则这两立体体积相等,这就是著名的祖暅公理(或刘祖原理)。祖暅应用这个原理,解决了刘徽尚未解决的球体积公式,该原理在西方直到十七世纪才由意大利数学家卡瓦列利(Bonaventura Cavalieri)发现,比祖暅晚一千一百多年。
祖暅历任太府卿等职,受家庭的影响,尤其是父亲的影响,他从小就热爱科学,对数学具有特别浓厚的兴趣,祖冲之在462年编制《大明历》就是在祖暅三次建议的基础上完成的。《缀术》一书经学者们考证,有些条目就是祖暅所作。祖暅终生读书专心致志,因走路时思考问题所以闹出了许多笑话,祖暅原理是关于球体体积的计算方法,这是祖暅一生最有代表性的发现。

祖暅
人物生平
祖冲之去世后,他在梁朝天监三年(公元504年)、八年、九年先后三次上书,建议采用他父亲编制的《大明历》,终于使父亲的遗愿得以实现。
祖暅的主要工作是修补编辑他父亲的数学著作《缀术》。他运用祖暅原理和由他创造的开立圆术,发展了他父亲的研究成果,巧妙地证得球的体积公式。他求得这一公式比意大利数学家卡瓦列利(Bonaventura Cavalieri,1589年—1647年)至少要早1100年。
祖暅还有不少其他科学发现,例如肯定北极星并非真正在北天极,而要偏离一度多等等,算得这些结果,同他丰富的数学知识是分不开的。
由于家学渊源,祖暅从小也钻研数学。祖暅之有巧思入神之妙,当他读书思考时,十分专一,即使有雷霆之声,他也听不到。有一次,他边走路边思考数学问题,走着走着,竟然撞了对面过来的仆射徐勉。“仆射”是很高的官,徐勉是朝廷要人,倒被这位年轻小子碰得够戗,不禁大叫起来,这时祖暅之方才醒悟。梁朝与北魏打仗,失败,祖暅之被魏方扣留,安排住进了驿站,很受优待。
祖暅还结识了一位天文学的爱好者信都芳,两人常常在一起研讨天文、数学,十分投机。祖暅之把自己的学问毫无保留地教给信都芳,使他有很大进步。祖暅之在科学上也取得了重大成就,《大明历》就是由于他的建议,才被梁朝采用。有的记载说,《缀术》有他的研究成果。他首次得出计算球体体积的公式,虽然比阿基米德晚了将近千年,但由于是与其父祖冲之运用独创的方法得出的,也不失是一种智慧结晶。他还研制了铜日圭、漏壶等精密观测仪器多种。
祖暅将数学知识传给了信都芳、毛栖成和自己的儿子祖皓,他们三位后来都成了数学家。
具体介绍
祖暅在梁朝担任过员外散骑侍郎、太府卿、南康太守、材官将军、奉朝请等职务。祖暅青年时代已对天文学和数学造诣很深,是祖冲之科学事业的继承人。他的主要贡献是修补编辑祖冲之的《缀术》,因此可以说《缀术》是他们父子共同完成的数学杰作。《九章算术》少广章中李淳风注所引述的“祖暅之开立圆术”,详细记载了祖冲之父子解决球体积问题的方法。
刘徽注释《九章算术》时指出球与外切“牟合方盖”的体积之比为a:4,但他未能求出牟合方盖的体积。祖冲之父子采用了“幂势既同,则积不容异”(两个等高的立体,如在等高处的截面积恒相等,则体积相等)的原理,解决了这一问题,从而给出球体积的正确公式。这一原理后人称之为“祖暅原理”,在西方,直到17世纪才由意大利数学家卡瓦列利重新发现。
在天文学方面,祖暅曾于504年、509年和510年三次上书建议采用祖冲之的《大明历》,最后一次终于实现了父亲的遗愿,《大明历》被梁武帝天监年间采用颁行。他还亲自监造八尺铜表,测量日影长度,并发现了北极星与北天极不动处相差一度有余,改进过当时通用的计时器——漏壶。祖暅的著作有《漏刻经》《天文录》等,但前者失传,后者仅存残篇。
原理
祖暅原理也就是“等积原理”
“等积原理”是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的。祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等。
等积原理的发现起源于《九章算术》中的答案是错误的。他提出的难方法是取每边为1寸的正方体棋子八枚,拼成一个边长为2寸的正方体,在正方体内画内切圆柱体,再在横向画一个同样的内切圆柱体。这样两个圆柱所包含的立体共同部分像两把上下对称的伞,刘徽将其取名为“牟合方盖”。(古时人称伞为“盖”,“牟”同侔,意即相合。)根据计算得出球体积是牟合方盖体的体积的四分之三,可是圆柱体又比牟合方盖大,但是《九章算术》中得出球的体积是圆柱体体积的四分之三,显然《九章算术》中的球体积计算公式是错误的。刘徽认为只要求出牟合方盖的体积,就可以求出球的体积。可怎么也找不出求导牟合方盖体积的途径。200多年后,祖暅出现了,他推导出了著名的“祖暅原理”,根据这一原理就可以求出牟合方盖的体积,然后再导出球的体积。
在现代的解析几何和测度应用中,祖暅原理是富比尼定理中的一个特例。西方的卡瓦列利没有对这条的严谨证明,只发表在1635年的Geometriaindivisibilibu以及1647年的ExercitationesGeometrica中,用以证明自己的MethodederIndivisibilie,以此方式可以计算某些立体的体积,甚至超越了阿基米德和克卜勒的成绩。这个定理引发了以面积计算体积的方法并成为了积分发展的一个重要步骤。
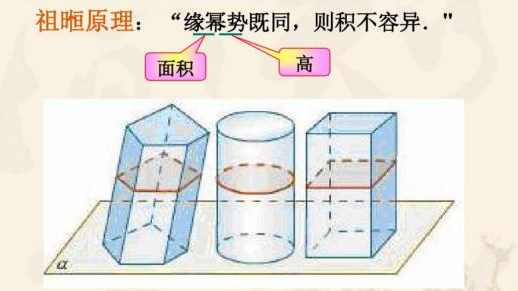
祖暅原理
圆柱体
如果垂直转轴切开圆柱体,设为半径,可以得到横切面面积为的圆形。根据祖暅原理,圆柱体的体积相等于方形面积相等于圆面积的立方体。
半球体
从其中一层以垂直表面的高横切半径为的半球体,根据勾股定理,求半径,横切面面积。对照立体是一个拥有与半球体相同表面积和高的立体,中间有一个圆锥体。高的对照立体环形切面有内圆周以及外圆周,因此两个立体都满足祖暅原理并且有相同体积。对照立体的体积便是圆柱体和圆锥体体积之差,所以成功利用这条有名的方程计算出半球体体积,从而导出球体体积公式。
微积分
祖暅原理背后的概念经常出现在微积分中。作为维度的一个例子,因此两条方程式在两个交点间的面积可以利用以下方程获得:实质上表示了函数图形和之间的面积与函数图形下的相同,而后者的交点距离与前者相等。由于现代数学中的积分和面积的互相关系,而体积可以通过微分计算,使祖暅原理变得更为少用。