解析几何,外文名英语:Analytic geometry,又称之为坐标几何,或者是卡氏几何,最早的时候叫做笛卡儿几何,借助于解析式进行图形研究的几何学分支。提出者是笛卡尔、费马等,分类是平面解析几何和立体解析几何。
解析几何通常使用二维的平面直角坐标系研究直线、圆、圆锥曲线、摆线、星形线等各种一般平面曲线,使用三维的空间直角坐标系来研究平面、球等各种一般空间曲面,同时研究它们的方程,并定义一些图形的概念和参数。坐标几何包括平面解析几何和立体解析几何两部分。平面解析几何通过平面直角坐标系,建立点与实数对之间的一一对应关系,以及曲线与方程之间的一一对应关系,运用代数方法研究几何问题,或用几何方法研究代数问题。

解析几何
历史
古希腊数学家梅内克缪斯(Menaechmus)的解题、证明方式与现在使用坐标系十分相似,以至于有时会认为他是解析几何的鼻祖。阿波罗尼奥斯在《论切触》中解题方式在现在被称之为单维解析几何;他使用直线来求得一点与其它点之间的比例。阿波罗尼奥斯在《圆锥曲线论》中进一步发展了这种方式,这种方式与解析几何十分相似,比起笛卡儿早了1800多年。他使用了参照线、直径、切线与现进所使用坐标系没有本质区别,即从切点沿直径所量的距离为横坐标,而与切线平行、并与数轴和曲线向交的线段为纵坐标。他进一步发展了横坐标与纵坐标之间的关系,即两者等同于夸张的曲线。然而,阿波罗尼奥斯的工作接近于解析几何,但它没能完成它,因为他没有将负数纳入系统当中。在此,方程是由曲线来确定的,而曲线不是由方程得出的。坐标、变量、方程不过是一些给定几何题的脚注罢了。
十一世纪波斯帝国数学家欧玛尔·海亚姆发现了几何与代数之间的密切联系,在求三次方程使用了代数和几何,取得了巨大进步。但最关键的一步由笛卡儿完成。
从传统意义上讲,解析几何是由勒内·笛卡儿创立的。笛卡儿的创举被记录在《几何学》(LaGeometrie)当中,在1637年与他的《方法论》一道发表。这些努力是以法语写成的,其中的哲学思想为创立无穷小提供了基础。最初,这些著作并没有得到认可,部分原因是由于其中论述的间断,方程的复杂所致。直到1649年,著作被翻译为拉丁语,并被冯·斯霍滕(vanSchooten)恭维后,才被大众所认可接受。
费马也为解析几何的发展做出了贡献。他的《平面与立体轨迹引论》虽然没有在生前发表,但手稿于1637年在巴黎出现,正好早于笛卡儿《方法论》一点。《引论》文字清晰,获得好评,为解析几何提供了铺垫。费马与笛卡儿方法的不同在于出发点。费马从代数公式开始,然后描述它的几何曲线,而笛卡儿从几何曲线开始,以方程的完结告终。结果,笛卡儿的方法可以处理更复杂的方程,并发展到使用高次多项式来解决问题。
发展
17世纪以来,由于航海、天文、力学、经济、军事、生产的发展,以及初等几何和初等代数的迅速发展,促进了坐标几何的建立,并被广泛应用于数学的各个分支。在坐标几何创立以前,几何与代数是彼此独立的两个分支。坐标几何的建立第一次真正实现了几何方法与代数方法的结合,使形与数统一起来,这是数学发展史上的一次重大突破。作为变量数学发展的第一个决定性步骤,坐标几何的建立对于微积分的诞生有着不可估量的作用。
基本理论

卡氏平面坐标系。四个点被标注了它们的坐标:(2,3)为绿色,(−3,1)为红色,(−1.5,−2.5)为蓝色,原点(0,0)为紫色。
坐标
在解析几何当中,平面给出了坐标系,即每个点都有对应的一对实数坐标。最常见的是笛卡儿坐标系,其中,每个点都有x-坐标对应水平位置,和y-坐标对应垂直位置。这些常写为有序对(x,y)。这种系统也可以被用在三维几何当中,空间中的每个点都以多元组呈现(x,y,z)。
坐标系也以其它形式出现。在平面中最常见的另类坐标系是极坐标系,其中每个点都以从原点出发的半径r和角度θ表示。在三维空间中,最常见的另类坐标系统是圆柱坐标系和球坐标系。
曲线方程
在解析几何当中,任何方程都包含确定面的子集,即方程的解集。例如,方程y=x在平面上对应的是所有x-坐标等于y-坐标的解集。这些点汇集成为一条直线,y=x被称为这道方程的直线。总而言之,线性方程中x和y定义线,一元二次方程定义圆锥曲线,更复杂的方程则阐述更复杂的形象。
通常,一个简单的方程对应平面上的一条曲线。但这不一定如此:方程x=x对应整个平面,方程x+y=0只对应(0,0)一点。在三维空间中,一个方程通常对应一个曲面,而曲线常常代表两个曲面的交集,或一条参数方程。方程x+y=r代表了是半径为r且圆心在(0,0)上的所有圆。
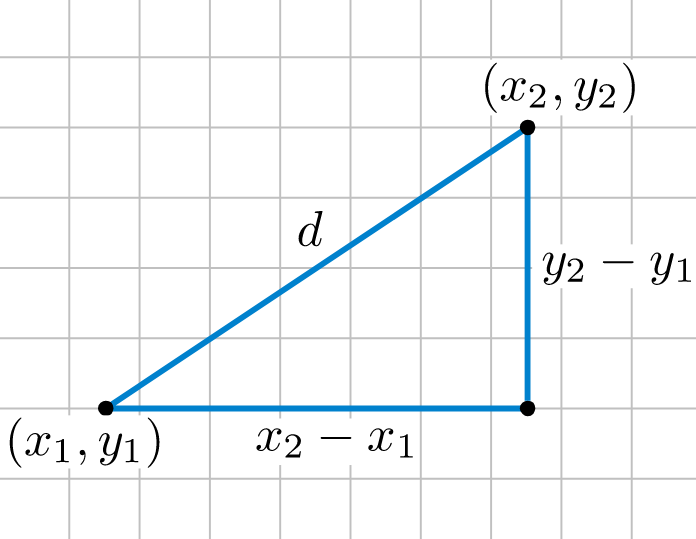
勾股定理的平面距离方程。
主题
解析几何中的重要问题:
向量空间
平面的定义
距离问题
点积求两个向量的角度
外积求一向量垂直于两个已知向量(以及它们的空间体积)
交点问题
Ax2+Bxy+Cy2+Dx+Ey+F=0{⁄displaystyleAx^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}.
现代解析几何
解析簇(analyticvariety)定义为几个解析函数的共同解集。类似与实数与复数的代数簇。任何复流形都是一种解析簇。由于解析簇可能有奇点,但不是所有解析簇都是复数。.
解析几何总体上来说等同与实数与复数代数几何,让-皮埃尔·塞尔在他的著作《代数几何与解析几何》(GéometrieAlgébriqueetGéométrieAnalytique)阐述了这个观点。然而,两个领域依然有其独特性,而证明方式也十分不同,代数几何也包括几何的有限特征。